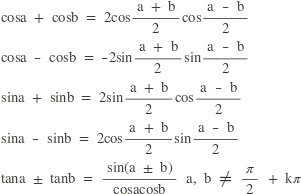I. Các hàm số lượng giác

1. Hàm số tuần hoàn

Hàm số f(x) có tập xác định D được gọi là hàm số tuần hoàn nếu có số T ≠ 0 sao cho:

a) ∀x ∈ D, đều có: x - T ∈ D và x + T ∈ D

b) ∀x ∈ D, đều có: f(x + T) = f(x)

Số T > 0 nhỏ nhất thỏa mãn các tính chất trên được gọi là chu kì của hàm số tuần hoàn f(x).

2. Các hàm số tuần hoàn thường gặp:

a, Hàm số y = sỉnx

Có tập xác định D = R, là hàm số lẻ, tuần hoàn với chu kì 2, lấy mọi giá trị thuộc đoạn [-1 ; 1].

b, Hàm số y = cosx

Có tập xác định D = R, là hàm số chẵn, tuần hoàn với chu kì 2, lấy mọi giá trị thuộc đoạn [-1; 1].

c, Hàm số y = tanx

Tập xác định D = {x ∈ R/x ≠  + k, k ∈ Z}, là hàm số lẻ tuần hoàn với chu kì , lấy mọi giá trị thuộc R.

d, Hàm số y = cotx

Tập xác định D = {x ∈ R/x ≠ k, k ∈ Z}, là hàm số lẻ, tuần hoàn với chu kì , lấy mọi giá trị thuộc R.

II. Công thức biến đổi

1. Tích thành tổng

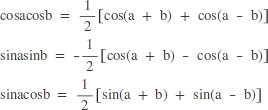
2. Tổng thành tích