Tích phân- Phương pháp đổi biến

PHƯƠNG PHÁP ĐỔI BIẾN SỐ

1. Đổi biến số loại 1: 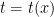$t=t(x)$

A. Phương pháp

Các bước thực hiện phép đổi biến số loại 1 để tính tích phân $I=\int_{a}^{b}{f(x)dx}$ .

+ Bước 1: Đặt $t=t(x)\Rightarrow dt=t'(x)dx$ .

Đổi cận:

+ Bước 2: Biến đổi $f(x)dx$ thành $g (t) d t$ .

+ Bước 3: Khi đó $I=\int_{t(a)}^{t(b)}{g(t)dt}$ (đơn giản hơn tích phân đã cho).

– Nếu hàm số $f(x)$ có chứa $\sqrt[n]{g(x)}$ thì đặt:

$t=\sqrt[n]{g(x)}\Leftrightarrow {{t}^{n}}=g(x)\Rightarrow n.{{t}^{n-1}}dt=g'(x)dx$

– Nếu hàm số $f(x)$ có chứa ${{(ax+b)}^{n}}$ thì đặt $t=ax+b\Rightarrow \left\{ \begin{array}{l}dt=adx\\x=\frac{t-b}{a}\end{array} \right.$ .

– Hàm lượng giác:

Nếu gặp $\int{f(\sin }x).\cos xdx$ thì đặt $t=\sin x$ .

Nếu gặp $\int{f(\cos x).\sin }xdx$ thì đặt $t=\cos x$ .

Nếu gặp $\int{f(\tan x)\frac{dx}{{{\cos }^{2}}x}}$ thì đặt $t=\tan x$ .

Nếu gặp $\int{f(\cot x)\frac{dx}{{{\sin }^{2}}x}}$ thì đặt $t=\cot x$ .

– Biểu thức có chứa logarit:

Thường gặp biểu thức có chứa $\frac{1}{x}$ và $\ln x$ . Khi đó đặt $t=\ln x$ hoặc $t=$ biểu thức có chứa $\ln x$ .

B. Bài tập ví dụ

Ví dụ 1.1: Cho đẳng thức $2\sqrt{3}.m-\int_{0}^{1}{\frac{4{{x}^{3}}}{{{({{x}^{4}}+2)}^{2}}}dx=0}$ . Khi đó $144{{m}^{2}}-1$ bằng

A. $-\frac{2}{3}$ . B. $-\frac{1}{3}$ . C. $\frac{1}{3}$ . D. $\frac{2}{3}$ .

Lời giải:

Để tính tích phân $I=\int_{0}^{1}{\frac{4{{x}^{3}}}{{{({{x}^{4}}+2)}^{2}}}dx}$ ta có thể làm trực tiếp bằng phương pháp vi phân, hoặc dùng phương pháp đặt ẩn phụ.

Cách 1 (Phương pháp vi phân)

Ta có $\int_{0}^{1}{\frac{4{{x}^{3}}}{{{({{x}^{4}}+2)}^{2}}}dx}=\int_{0}^{1}{\frac{d({{x}^{4}})}{{{({{x}^{4}}+2)}^{2}}}=\left. \left( -\frac{1}{{{x}^{4}}+2} \right) \right|_{0}^{1}}$

$=-\frac{1}{3}-(-\frac{1}{2})=\frac{1}{6}$ .

Cách 2 (Phương pháp đổi biến)

Đặt $t={{x}^{4}}+2\Rightarrow dt=4{{x}^{3}}dx$ .

Đổi cận: $x=0\Rightarrow t=2$ .

$x=1\Rightarrow t=3$ .

$\Rightarrow I=\int_{2}^{3}{\frac{dt}{{{t}^{2}}}=-\left. \frac{1}{t} \right|_{2}^{3}=-\frac{1}{3}+\frac{1}{2}=\frac{1}{6}}$ .

Khi đó $2\sqrt{3}m-\int_{0}^{1}{\frac{4{{x}^{3}}}{{{({{x}^{4}}+2)}^{2}}}dx=0\Leftrightarrow 2\sqrt{3}m-\frac{1}{6}=0}$ $\Leftrightarrow m=\frac{\sqrt{3}}{36}\Leftrightarrow 144{{m}^{2}}-1=-\frac{2}{3}$ .

Chọn A.

Ví dụ 1.2: Cho biết $\displaystyle \int\limits_{-1}^{5}{f\left( x \right)\text{d}x}=15$ . Tính giá trị của $P=\int\limits_{0}^{2}{\left[ f\left( 5-3x \right)+7 \right]\text{d}x}$

A. $P=15$ B. $P=37$ C. $P=27$ D. $P=19$

Lời giải:

$P=\int\limits_{0}^{2}{\left[ f\left( 5-3x \right)+7 \right]\text{d}x}=\int\limits_{0}^{2}{f\left( 5-3x \right)\text{d}x}+\int\limits_{0}^{2}{\text{7d}x}$

Xét $\int_{0}^{2}{f(5-3x)dx}$ , đặt $t=5-3x\Rightarrow dt=-3dx$ .

Đổi cận: $x=0\Rightarrow t=5,\,\,x=2\Rightarrow t=1$ .

$\Rightarrow \int_{0}^{2}{f(5-3x)dx}=-\frac{1}{3}\int\limits_{5}^{1}{f\left( x \right)\text{d}x}+7\left( 2-0 \right)=5+14=9$ .

Đáp án D

Ví dụ 1.3: Biết rằng $I=\int_{0}^{\frac{\pi }{2}}{\frac{\sin 2x\cos x}{1+\cos x}dx}=a\ln 2+b$ với $a,b$ là các số nguyên. Tính $P=2{{a}^{2}}+3{{b}^{3}}$ .

A. $5$ . B. 7. C. 8. D. 11.

Lời giải:

$I=\int_{0}^{\frac{\pi }{2}}{\frac{\sin 2x\cos x}{1+\cos x}dx}=\int_{0}^{\frac{\pi }{2}}{\frac{2\sin x{{\cos }^{2}}x}{1+\cos x}}dx$

Cách 1 (Phương pháp vi phân)

$\begin{array}{l}I=-2\int_{0}^{\frac{\pi }{2}}{\frac{{{\cos }^{2}}x}{1+\cos x}d(\cos x)}=-2\int_{0}^{\frac{\pi }{2}}{\left( \cos x-1+\frac{1}{1+\cos x} \right)}d(\cos x)\\=\left. (-{{\cos }^{2}}x+2x-2\ln |1+\cos x|) \right|_{0}^{\frac{\pi }{2}}=2\ln 2-1\end{array}$

Cách 2 (Phương pháp đổi biến)

Đặt $t=\cos x\Rightarrow dt=-\sin xdx$ .

Đổi cận: $x=0\Rightarrow t=1;\,\,x=\frac{\pi }{2}\Rightarrow t=0$ .

$\Rightarrow I=\int_{1}^{0}{\frac{-2{{t}^{2}}}{1+t}dt}=\int_{0}^{1}{(2t-2+\frac{2}{1+t})dt}$ $=\left. ({{t}^{2}}-2t+2\ln |1+t|) \right|_{0}^{1}=-1+2\ln 2$ .

Do đó $a=2;b=-1\Rightarrow P=2{{a}^{2}}+3{{b}^{3}}=11$ .

Chọn D.

Ví dụ 1.4: Biết rằng $I=\int_{1}^{e}{\frac{2\ln x+1}{x{{(\ln x+1)}^{2}}}dx}=a\ln 2-\frac{b}{c}$ với $a,b,c$ là các số nguyên dương và $\frac{b}{c}$ là phân số tối giản. Tính $S=a+b+c$ .

A. $S=3$ . B. $S=5$ . C. $S=7$ . D. $S=10$ .

Lời giải:

Đặt $t=\ln x\Rightarrow dt=\frac{dx}{x}$ .

Đổi cận: $x=1\Rightarrow t=0;\,\,x=e\Rightarrow t=1$ .

$\Rightarrow I=\int_{0}^{1}{\frac{2t+1}{{{(t+1)}^{2}}}dt}=\int_{0}^{1}{\left( \frac{2}{t+1}-\frac{1}{{{(t+1)}^{2}}} \right)dt}$ $=\left. \left[ 2\ln |t+1|+\frac{1}{t+1} \right]\, \right|_{0}^{1}=2\ln 2-\frac{1}{2}$ .

$\Rightarrow a=2;\,b=1;\,c=1\Rightarrow S=5$ .

Chọn B.

Ví dụ 1.5: Xét tích phân $I=\int_{0}^{\sqrt{3}}{{{x}^{5}}\sqrt{{{x}^{2}}+1}dx}=\frac{a}{b}$ là một số phân số tối giản. Tính hiệu $a-b$ .

A. $743$ . B. $-64$ . C. $27$ . D. $-207$ .

Lời giải:

Đặt $t=\sqrt{{{x}^{2}}+1}\Rightarrow {{t}^{2}}={{x}^{2}}+1\Rightarrow tdt=xdx$ .

Đổi cận $x=0\Rightarrow t=1;\,\,x=\sqrt{3}\Rightarrow t=2$ .

Khi đó $I=\int_{1}^{2}{{{({{t}^{2}}-1)}^{2}}.{{t}^{2}}dt}=\int_{1}^{2}{({{t}^{6}}-2{{t}^{4}}+{{t}^{2}})dt}$ $=\left. \left( \frac{{{t}^{2}}}{7}-2\frac{{{t}^{5}}}{5}+\frac{{{t}^{3}}}{3} \right) \right|_{1}^{2}=\frac{848}{105}=\frac{a}{b}$ .

Suy ra $a-b=743$ . Chọn A.

2. Đổi biến số loại 2: $x=x(t)$

A. Phương pháp

Các bước thực hiện phép đổi biến số loại 2 để tính tích phân $I=\int_{a}^{b}{f(x)dx}$ .

+ Bước 1: Đặt $x=x(t)\Rightarrow dx=x'(t)dt$ .

Đổi cận:

+ Bước 2: Biến đổi $f(x)dx$ thành $g(t)dt$ .

+ Bước 3: Khi đó $I=\int_{t(a)}^{t(b)}{g(t)dt}$ (đơn giản hơn tích phân đã cho).

- Nếu hàm số $f(x)$ có chứa $\sqrt{{{a}^{2}}-{{x}^{2}}}$ thì đặt

$x=a\sin t\Rightarrow \left\{ \begin{array}{l}dx=d(a\sin t)=a\cos t.dt\\\sqrt{{{a}^{2}}-{{x}^{2}}}=\sqrt{{{a}^{2}}-{{a}^{2}}{{\sin }^{2}}t}=a\cos t\end{array} \right.$

- Nếu hàm $f(x)$ có chứa $\sqrt{{{a}^{2}}+{{x}^{2}}}$ thì đặt

$\displaystyle x=a\tan t\Rightarrow \left\{ \begin{array}{l}dx=d(a\tan t)=\frac{adt}{{{\cos }^{2}}t}=a(1+{{\tan }^{2}}t)dt\\\sqrt{{{a}^{2}}+{{x}^{2}}}=\sqrt{{{a}^{2}}+{{a}^{2}}{{\tan }^{2}}t}=\frac{|a|}{\cos t}\end{array} \right.$

- Nếu hàm $f(x)$ có chứa $\sqrt{{{x}^{2}}-{{a}^{2}}}$ thì đặt $x=\frac{a}{\sin t}\Rightarrow \left\{ \begin{array}{l}dx=d(\frac{a}{\sin t})=-\frac{a\cos t.dt}{{{\sin }^{2}}t}\\\sqrt{{{x}^{2}}-{{a}^{2}}}=\sqrt{\frac{{{a}^{2}}}{{{\sin }^{2}}t}-{{a}^{2}}}=\frac{|a|}{\cot t}\end{array} \right.$

- Nếu hàm $f(x)$ có chứa ${{(1+{{x}^{2}})}^{k}}$ thì đặt

$x=\tan t\Rightarrow \left\{ \begin{array}{l}dx=d(\tan t)=\frac{dt}{{{\cos }^{2}}t}\\{{(1+{{x}^{2}})}^{k}}={{(1+{{\tan }^{2}}x)}^{k}}=\frac{1}{{{\cos }^{2k}}t}\end{array} \right.$

B. Bài tập ví dụ

Ví dụ 2.1: Biết rằng $I=\int_{0}^{\frac{1}{2}}{\sqrt{1-{{x}^{2}}}dx}=\frac{\pi }{a}+\frac{\sqrt{3}}{b}$ với $a,b$ là các số nguyên. Tính $P=a+b$ .

A. 10. B. 12. C. 15. D. 20.

Lời giải:

Đặt .

Đổi cận $x=0\Rightarrow t=0;\,\,x=\frac{1}{2}\Rightarrow t=\frac{\pi }{6}$ .

$\displaystyle \Rightarrow I=\int_{0}^{\frac{\pi }{6}}{\sqrt{1-{{\sin }^{2}}t}.\cos tdt}=\int_{0}^{\frac{\pi }{6}}{{{\cos }^{2}}tdt}$

$\displaystyle =\frac{1}{2}\int_{0}^{\frac{\pi }{6}}{(1+\cos 2t)dt}=\left. \left( \frac{1}{2}x+\frac{1}{4}\sin 2t \right) \right|_{0}^{\frac{\pi }{6}}=\frac{\pi }{12}+\frac{\sqrt{3}}{8}$ .

Do đó .

Chọn D.

Ví dụ 2.2: Tính các tích phân sau

a) $I=\int_{0}^{\frac{\pi }{4}}{\frac{{{x}^{2}}dx}{\sqrt{1-{{x}^{2}}}}}$ . b) . c) $I=\int_{0}^{3}{\frac{dx}{9+{{x}^{2}}}}$ .

Lời giải:

a) Đặt $x=\sin t\Rightarrow dx=\cos tdt$ .

Đổi cận $x=0\Rightarrow t=0;\,x=\frac{\sqrt{2}}{2}\Rightarrow t=\frac{\pi }{4}\,$ .

$\displaystyle \begin{array}{l}\Rightarrow I=\int_{0}^{\frac{\pi }{4}}{\frac{{{\sin }^{2}}t\cos t}{\sqrt{1-{{\sin }^{2}}t}}dt=\int_{0}^{\frac{\pi }{4}}{\frac{{{\sin }^{2}}t\cos t}{\cos t}dt}}\\=\int_{0}^{\frac{\pi }{4}}{{{\sin }^{2}}tdt}=\frac{1}{2}\int_{0}^{\frac{\pi }{4}}{(1-\cos 2t)dt}\\=\left. \left( \frac{1}{2}t-\frac{1}{4}\sin 2t \right) \right|_{0}^{\frac{\pi }{4}}=\frac{\pi }{8}-\frac{1}{4}\end{array}$

b) Đặt $x=\sqrt{3}\tan t\Rightarrow dx=\frac{\sqrt{3}}{{{\cos }^{2}}t}$ .

Đổi cận $x=1\Rightarrow t=\frac{\pi }{6};\,\,x=\sqrt{3}\Rightarrow t=\frac{\pi }{4}$ .

$\displaystyle \begin{array}{l}\Rightarrow I=\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{\sqrt{9+9{{\tan }^{2}}t}}{3{{\tan }^{2}}t{{\cos }^{2}}t}dt=3\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{dt}{\cos t.{{\cos }^{2}}t.\frac{{{\sin }^{2}}t}{{{\cos }^{2}}t}}}}\\=3\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{dt}{\cos t.{{\sin }^{2}}t}}=3\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{\cos tdt}{{{\cos }^{2}}t.{{\sin }^{2}}t}}\\=3\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{d(\sin t)}{(1-{{\sin }^{2}}t).{{\sin }^{2}}t}}=3\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\left( \frac{1}{1-{{\sin }^{2}}t}+\frac{1}{{{\sin }^{2}}t} \right)d(\sin t)}\\=3\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\left( \frac{1}{2(1-\sin t)}+\frac{1}{2(1+\sin t)}+\frac{1}{{{\sin }^{2}}t} \right)d(\sin t)}\\=\frac{3}{2}\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{d(\sin t)}{1-\sin t}+\frac{3}{2}\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{d(\sin t)}{1+\sin t}+3\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}{\frac{d(\sin t)}{{{\sin }^{2}}t}}}}\\=\frac{3}{2}\ln \left. \left| \frac{1+\sin t}{1-\sin t} \right|\, \right|_{\frac{\pi }{6}}^{\frac{\pi }{4}}-\left. \frac{3}{\sin t} \right|_{\frac{\pi }{6}}^{\frac{\pi }{4}}\\=\frac{3}{2}\left( \ln \frac{2+\sqrt{2}}{2-\sqrt{2}}-\ln 3 \right)+6-\frac{6}{\sqrt{2}}\end{array}$

c) Đặt $x=3\tan t\Rightarrow dx=\frac{3dt}{{{\cos }^{2}}t}=3(1+{{\tan }^{2}}t)dt$ .

Đổi cận $x=0\Rightarrow t=0;\,x=3\Rightarrow t=\frac{\pi }{4}$ .

$\Rightarrow I=\int_{0}^{\frac{\pi }{4}}{\frac{(1+{{\tan }^{2}}t)dt}{9+9{{\tan }^{2}}t}=\frac{1}{3}t|_{0}^{\frac{\pi }{4}}=\frac{\pi }{12}}$ .

3. Đổi biến dựa vào cận

A. Phương pháp

Đối với tích phân có dạng $I=\int_{-a}^{a}{f(x)dx}$ , ta sử dụng phép đổi biến $x=-t$ .

Khi đó $I=\int_{-a}^{a}{f(x)dx}=\int_{-a}^{0}{f(x)dx}+\int_{0}^{a}{f(x)dx}$

Xét tích phân ${{I}_{1}}=\int_{-a}^{0}{f(x)dx}$ :

Đặt $x=-t\Rightarrow dx=-dt$ .

Đổi cận: $x=-a\Rightarrow t=a,\,\,x=0\Rightarrow t=0$ .

$\Rightarrow I=\int_{a}^{0}{f(-t)d(-t)}+\int_{0}^{a}{f(x)dx}$ .

Nhận xét:

- Nếu $f(x)$ liên tục và là hàm lẻ trên $\displaystyle \text{ }\!\![\!\!\text{ }-a;a]$ thì $I = \int_{- a}^{a} f (x) d x$ .

- Nếu $f(x)$ liên tục và là hàm chẵn trên đoạn $\displaystyle \text{ }\!\![\!\!\text{ }-a;a]$ thì $I = \int_{- a}^{a} f (x) d x = 2 \int_{0}^{a} f (x) d x$ .

B. Bài tập ví dụ

Ví dụ 3.1 (THPT Bắc Duyên Hà – Thái Bình 2017 Lần 2) Cho hàm số $f(x)$ chẵn, liên tục trên $\mathbb{R}$ và $\int_{-2}^{2}{f(x)dx}=3$ . Tính $I=\int_{\frac{1}{3}}^{1}{f(3x-1)dx}$ .

A. $\frac{1}{3}$ . B. $\frac{3}{2}$ . C. $\frac{1}{2}$ . D. 3.

Lời giải:

Đặt $t=3x-1\Rightarrow dt=3dx\Rightarrow dx=\frac{1}{3}dt$ .

Ta có $I=\int_{0}^{2}{f(t).\frac{1}{3}dt}\Rightarrow 3I=\int_{0}^{1}{f(x)dx}$ .

Mặt khác, đặt $u=-x\Rightarrow du=-dx$ . Do $f(x)$ là hàm số chẵn nên $f(-x)=f(x)$ .

Suy ra $\int_{-2}^{0}{f(x)dx}=-\int_{0}^{2}{f(-u)du}=\int_{0}^{2}{f(u)du}$

$\Rightarrow 3=\int_{-2}^{2}{f(x)dx}=\int_{-2}^{0}{f(x)dx}+\int_{0}^{2}{f(x)dx}$ $=2\int_{0}^{2}{f(x)dx}=6I\Rightarrow I=\frac{1}{2}$ .

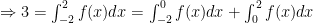
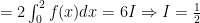Chọn C.

Ví dụ 3.2: Cho $a$ là một số thực khác 0, kí hiệu $b=\int_{-a}^{a}{\frac{{{e}^{x}}}{x+2a}dx}$ . Tính $I=\int_{0}^{2a}{\frac{dx}{(3a-x){{e}^{x}}}}$ theo $a$ và $b$ .

A. $a$ . B. $\frac{b}{{{e}^{a}}}$ C. $b$ . D. ${{e}^{b}}.b$ .

Lời giải:

Đặt $t=a-x\Rightarrow \left\{ \begin{array}{l}dx=-dt\\3a-x=t+2a\end{array} \right.$ .

Đổi cận: $x=0\Rightarrow t=a;\,x=2a\Rightarrow t=-a$ .

Khi đó $I=\int_{a}^{-a}{\frac{dt}{(t+2a){{e}^{a-1}}}=\int_{-a}^{a}{\frac{{{e}^{x}}}{(x+2a){{e}^{x}}}dx}}$ .

Mà $b=\int_{-a}^{a}{\frac{{{e}^{x}}}{x+2a}dx}\Rightarrow I=\frac{b}{{{e}^{a}}}$ .

Chọn B.

Ví dụ 3.3: Tính tích phân $I=\int_{-1}^{1}{\frac{\cos xdx}{{{e}^{x}}+1}}$ .

Lời giải:

Cách 1:

$I=\int_{-1}^{0}{\frac{\cos xdx}{{{e}^{x}}+1}+\int_{0}^{1}{\frac{\cos xdx}{{{e}^{x}}+1}={{I}_{1}}+{{I}_{2}}}}$ trong đó ${{I}_{1}}=\int_{-1}^{0}{\frac{\cos xdx}{{{e}^{x}}+1}}$ , ${{I}_{2}}=\int_{0}^{1}{\frac{\cos xdx}{{{e}^{x}}+1}}$ .

Xét ${{I}_{1}}=\int_{-1}^{0}{\frac{\cos xdx}{{{e}^{x}}+1}}$ , đặt $t=-x\Rightarrow dt=-dx$ .

Đổi cận $x=-1\Rightarrow t=1;\,x=0\Rightarrow t=0$ .

Khi đó ${{I}_{1}}=-\int_{1}^{0}{\frac{\cos tdt}{{{e}^{-t}}+1}=\int_{0}^{1}{\frac{\cos tdt}{\frac{1}{{{e}^{t}}}+1}=\int_{0}^{1}{\frac{{{e}^{x}}.\cos xdx}{1+{{e}^{x}}}}}}$ .

Suy ra $I=\int_{0}^{1}{\frac{{{e}^{x}}\cos xdx}{1+{{e}^{x}}}+\int_{0}^{1}{\frac{\cos xdx}{{{e}^{x}}+1}}=\int_{0}^{1}{\frac{({{e}^{x}}+1)\cos xdx}{{{e}^{x}}+1}}}$ $=\int_{0}^{1}{\cos xdx}=\sin x|_{0}^{1}=\sin 1$ .

Cách 2:

Đặt $t=-x\Rightarrow dt=-dx$ .

Đổi cận $x=-1\Rightarrow t=1;\,x=1\Rightarrow t=-1$ .

Khi đó $I=-\int_{1}^{-1}{\frac{\cos tdt}{{{e}^{-t}}+1}=\int_{-1}^{1}{\frac{\cos tdt}{\frac{1}{{{e}^{t}}}+1}}}$ $=\int_{-1}^{1}{\frac{{{e}^{t}}.\cos tdt}{1+{{e}^{t}}}}=\int_{-1}^{1}{\frac{{{e}^{x}}\cos xdx}{1+{{e}^{x}}}}$

$\displaystyle \begin{array}{l}\Rightarrow 2I=I+I=\int_{-1}^{1}{\frac{\cos xdx}{{{e}^{x}}+1}+\int_{-1}^{1}{\frac{{{e}^{x}}\cos xdx}{{{e}^{x}}+1}}}\\=\int_{-1}^{1}{\cos xdx}=\sin x|_{-1}^{1}=2\sin 1\end{array}$ .